
|
–ü–æ–∫–∞ —á–µ–ª–æ–≤–µ–∫ –Ω–µ —Ä–∞–∑–≤–∏–ª –≤ —Å–µ–±–µ —Å–æ–≤–µ—Ä—à–µ–Ω–Ω–æ–≥–æ —á—É–≤—Å—Ç–≤–∞ —Å–ø—Ä–∞–≤–µ–¥–ª–∏–≤–æ—Å—Ç–∏, –µ–º—É –ø—Ä–µ–¥–ø–æ—á—Ç–∏—Ç–µ–ª—å–Ω–µ–µ –æ—à–∏–±–∞—Ç—å—Å—è –≤—Å–ª–µ–¥—Å—Ç–≤–∏–µ –∏–∑–±—ã—Ç–∫–∞ —Å–Ω–∏—Å—Ö–æ–¥–∏—Ç–µ–ª—å–Ω–æ—Å—Ç–∏, —á–µ–º —Å–æ–≤–µ—Ä—à–∞—Ç—å –º–∞–ª–µ–π—à—É—é –Ω–µ—Å–ø—Ä–∞–≤–µ–¥–ª–∏–≤–æ—Å—Ç—å. –ü–∏—Å—å–º–∞ –ú–∞—Å—Ç–µ—Ä–æ–≤ –ú—É–¥—Ä–æ—Å—Ç–∏, 108 |

–¶–µ–ª—å –¥–æ–∫–ª–∞–¥–∞ — –ø–æ–∫–∞–∑–∞—Ç—å, —á—Ç–æ –±–µ—Å–∫–æ–Ω–µ—á–Ω–æ—Å—Ç—å –Ω–µ –æ—Ç–≤–ª–µ—á—ë–Ω–Ω–æ–µ –ø–æ–Ω—è—Ç–∏–µ, —á—Ç–æ –ø—Ä–∏ —Ä–µ—à–µ–Ω–∏–∏ –º–∞—Ç–µ–º–∞—Ç–∏—á–µ—Å–∫–∏—Ö –∑–∞–¥–∞—á –ø—Ä–∏–º–µ–Ω—è—é—Ç—Å—è –º–µ—Ç–æ–¥—ã, –æ—Å–Ω–æ–≤–∞–Ω–Ω—ã–µ –Ω–∞ –±–µ—Å–∫–æ–Ω–µ—á–Ω–æ—Å—Ç–∏.
–ë–µ—Å–ø—Ä–µ–¥–µ–ª—å–Ω–æ—Å—Ç—å, –∏–Ω–∞—á–µ –≥–æ–≤–æ—Ä—è, «—Ä–∞–∑–≤–∏—Ç–∏–µ –≤ –ë–µ—Å–∫–æ–Ω–µ—á–Ω–æ—Å—Ç—å» (–ë—Ä–∞—Ç—Å—Ç–≤–æ, 8) –≤—Å–µ—Ö –ø–æ–Ω—è—Ç–∏–π, –æ—Ç–Ω–æ—Å–∏—Ç—Å—è –∫ –æ—Å–Ω–æ–≤–Ω—ã–º –ø—Ä–∏–Ω—Ü–∏–ø–∞–º –£—á–µ–Ω–∏—è –ñ–∏–≤–æ–π –≠—Ç–∏–∫–∏. –ü—Ä–∏–Ω—Ü–∏–ø —Ç—Ä—É–¥–Ω—ã–π, —É—Å–∫–æ–ª—å–∑–∞—é—â–∏–π –æ—Ç –ø–æ–Ω–∏–º–∞–Ω–∏—è. –î–µ–π—Å—Ç–≤–∏—Ç–µ–ª—å–Ω–æ, –≤ –æ–∫—Ä—É–∂–∞—é—â–µ–º –Ω–∞—Å –º–∏—Ä–µ —Ç—Ä—É–¥–Ω–æ —É–∫–∞–∑–∞—Ç—å –Ω–∞ –∫–∞–∫–æ–π-–ª–∏–±–æ –ø—Ä–µ–¥–º–µ—Ç –∏ —Å–∫–∞–∑–∞—Ç—å: —Å–º–æ—Ç—Ä–∏—Ç–µ, –∑–¥–µ—Å—å –±–µ—Å–∫–æ–Ω–µ—á–Ω–æ—Å—Ç—å. –ù–æ –≤ –º–∞—Ç–µ–º–∞—Ç–∏–∫–µ —ç—Ç–æ –ø—Ä–æ—â–µ, –≤–µ–¥—å –º–∞—Ç–µ–º–∞—Ç–∏–∫–∞ ‚Äî —ç—Ç–æ –Ω–∞—É–∫–∞, –∏–º–µ—é—â–∞—è –¥–µ–ª–æ —Å –≤–µ—á–Ω—ã–º–∏ –∏—Å—Ç–∏–Ω–∞–º–∏.
И Учение Живой Этики утверждает, что «самая близкая духу наука будет высшая математика, если она понята правильно. Так отвлечённость делается реальностью. Туман знания может просветиться Беспредельностью. Конечно, мы должны стремиться ко всему, что может выводить наше сознание за пределы планеты. Только так можно понимать истинные ценности» (Иерархия, 162).
Математика даёт чрезвычайно богатый материал для нашей темы, потому что во многих математических рассуждениях используются бесконечно малые или бесконечно большие величины. Более того, такие рассуждения составляют основу современной математики. Но мы сейчас не имеем возможности углубиться в основы математики, а вместо этого рассмотрим несколько простых примеров, помогающих более или менее наглядно ощутить, «пощупать» математическую бесконечность.
В школьной программе есть тема «Сумма бесконечной геометрической прогрессии». Выберем какое-нибудь число, положительное и меньшее единицы, обозначим его буквой a и рассмотрим следующий бесконечный ряд чисел: 1, а, a2, a3 и так далее — это и есть геометрическая прогрессия. Числа в этом ряду становятся всё меньше и меньше. Оказывается, что если сложить весь этот бесконечный набор чисел, то получится простой ответ:
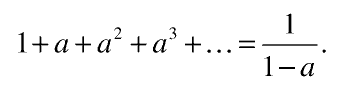
–í–æ–∑–Ω–∏–∫–∞–µ—Ç –≤–æ–ø—Ä–æ—Å: –∫–æ–º—É –∏, –≥–ª–∞–≤–Ω–æ–µ, –∑–∞—á–µ–º –º–æ–∂–µ—Ç –ø–æ–Ω–∞–¥–æ–±–∏—Ç—å—Å—è —Å–ª–æ–∂–µ–Ω–∏–µ –±–µ—Å–∫–æ–Ω–µ—á–Ω–æ –º–Ω–æ–≥–∏—Ö —á–∏—Å–µ–ª?
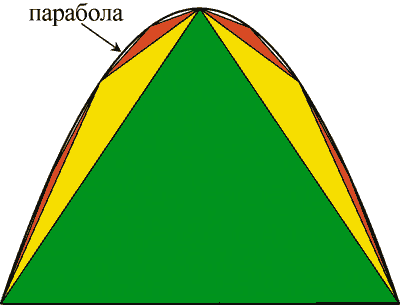
По-видимому, первым, кому это понадобилось, был Архимед. Он использовал бесконечный числовой ряд, чтобы найти площадь сегмента параболы (рис. 1). Парабола — кривая, известная из школьной программы. Площадь, которая нас интересует, заключена между параболой и прямой линией.
¬Ý
Как действовал Архимед? На первом шаге он вписал в этот кусок параболы треугольник максимальной высоты и нашёл его площадь. По бокам от треугольника остались два маленьких незакрытых сегмента. На втором шаге в них тоже вписываются треугольники максимальной высоты и находится их площадь. Третий шаг — вставить четыре треугольника в четыре маленьких «окошка», оставшихся незакрытыми, и так далее.
–ù–æ —Ç–µ–ø–µ—Ä—å —É–∂–µ –≤–∏–¥–Ω–æ, —á—Ç–æ –Ω–∏ –∑–∞ –∫–∞–∫–æ–µ –∫–æ–Ω–µ—á–Ω–æ–µ —á–∏—Å–ª–æ —à–∞–≥–æ–≤ –≤—Å—é –ø–ª–æ—â–∞–¥—å –ø–æ–¥ –ø–∞—Ä–∞–±–æ–ª–æ–π –∏—Å—á–µ—Ä–ø–∞—Ç—å –Ω–µ –ø–æ–ª—É—á–∏—Ç—Å—è, —Ç–æ –µ—Å—Ç—å –Ω–∏ –∑–∞ —Ç—ã—Å—è—á—É —à–∞–≥–æ–≤, –Ω–∏ –∑–∞ –º–∏–ª–ª–∏–æ–Ω –º—ã –Ω–µ –¥–æ–±–µ—Ä—ë–º—Å—è –¥–æ —Ç–æ—á–Ω–æ–≥–æ –æ—Ç–≤–µ—Ç–∞. –¢—É—Ç-—Ç–æ –∏ –≤—ã—Ä—É—á–∞–µ—Ç —Å—É–º–º–∞ –≥–µ–æ–º–µ—Ç—Ä–∏—á–µ—Å–∫–æ–π –ø—Ä–æ–≥—Ä–µ—Å—Å–∏–∏.
Оказывается, что если площадь большого зелёного треугольника принять за 1, то жёлтые треугольники занимают площадь 1/4, маленькие красные треугольнички — площадь 1/16 и так далее. Получается как раз геометрическая прогрессия, сумму которой можно найти по формуле, приведённой выше (подставив в неё a = 1/4):
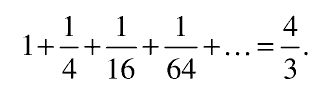
–ü–æ–ª—É—á–∞–µ–º –ø—Ä–æ—Å—Ç–æ–π –æ—Ç–≤–µ—Ç ‚Äî –ø–ª–æ—â–∞–¥—å —Ñ–∏–≥—É—Ä—ã —Ä–∞–≤–Ω–∞ 4/3 –æ—Ç –ø–ª–æ—â–∞–¥–∏ –∑–µ–ª—ë–Ω–æ–≥–æ —Ç—Ä–µ—É–≥–æ–ª—å–Ω–∏–∫–∞. –¢–∞–∫–æ–π —Å–ø–æ—Å–æ–± –≤—ã—á–∏—Å–ª–µ–Ω–∏—è –ø–ª–æ—â–∞–¥–µ–π –Ω–∞–∑—ã–≤–∞–µ—Ç—Å—è –º–µ—Ç–æ–¥–æ–º –∏—Å—á–µ—Ä–ø—ã–≤–∞–Ω–∏—è, –ø—Ä–∏–¥—É–º–∞–ª–∏ –µ–≥–æ –º–∞—Ç–µ–º–∞—Ç–∏–∫–∏ –î—Ä–µ–≤–Ω–µ–π –ì—Ä–µ—Ü–∏–∏. –ù–æ –ø—Ä–∏–º–µ–Ω—è—Ç—å –µ–≥–æ –Ω–µ —Ç–∞–∫-—Ç–æ –ø—Ä–æ—Å—Ç–æ, –ø–æ—ç—Ç–æ–º—É –ª–µ—Ç —á–µ—Ç—ã—Ä–µ—Å—Ç–∞ –Ω–∞–∑–∞–¥ –±—ã–ª –∏–∑–æ–±—Ä–µ—Ç—ë–Ω —Å–ø–æ—Å–æ–± –ø–æ–ø—Ä–æ—â–µ. –Ý–∞–∑–æ–±—å—ë–º –Ω–∞—à—É —Ñ–∏–≥—É—Ä—É –Ω–∞ –º–Ω–æ–≥–æ —É–∑–∫–∏—Ö –ø—Ä—è–º–æ—É–≥–æ–ª—å–Ω–∏–∫–æ–≤ ‚Äî —Ç–æ—á–Ω–µ–µ –≥–æ–≤–æ—Ä—è, –±–µ—Å–∫–æ–Ω–µ—á–Ω–æ –º–Ω–æ–≥–æ –±–µ—Å–∫–æ–Ω–µ—á–Ω–æ —É–∑–∫–∏—Ö –ø—Ä—è–º–æ¬≠—É–≥–æ–ª—å–Ω–∏–∫–æ–≤. –ù–∞–π–¥—ë–º –ø–ª–æ—â–∞–¥—å –∫–∞–∂–¥–æ–≥–æ —Ç–∞–∫–æ–≥–æ —Å—Ç–æ–ª–±–∏–∫–∞ –∏ —Å–ª–æ–∂–∏–º –∏—Ö –ø–ª–æ—â–∞–¥–∏. –≠—Ç–æ –∏ –Ω–∞–∑—ã–≤–∞–µ—Ç—Å—è ¬´–≤–∑—è—Ç—å –∏–Ω—Ç–µ–≥—Ä–∞–ª¬ª.
Отсюда видно, что само понятие площади криволинейной фигуры — не такое уж простое: в скрытом виде оно содержит в себе бесконечность. Как же вы тогда узнаете, сколько у вас квадратных метров жилплощади, если, допустим, в вашей квартире есть такое закругление, как на рис. 1. Наверное, будете дробить эту площадь на прямо­угольники, постепенно приближаясь к точному ответу. Но чтобы достичь этого точного ответа, в любом случае понадобится бесконечно мелкое дробление.
–ó–¥–µ—Å—å –≤–æ–∑–Ω–∏–∫–∞–µ—Ç –∏–Ω—Ç–µ—Ä–µ—Å–Ω—ã–π –≤–æ–ø—Ä–æ—Å: –∞ –Ω—É–∂–µ–Ω –ª–∏ –¥–ª—è –ø—Ä–∞–∫—Ç–∏—á–µ—Å–∫–∏—Ö –Ω—É–∂–¥ –∞–±—Å–æ–ª—é—Ç–Ω–æ —Ç–æ—á–Ω—ã–π —Ä–µ–∑—É–ª—å—Ç–∞—Ç? –¢–æ—Ç –∂–µ –ê—Ä—Ö–∏–º–µ–¥ –º–æ–≥ –±—ã –æ—Å—Ç–∞–Ω–æ–≤–∏—Ç—å—Å—è, —Å–∫–∞–∂–µ–º, –Ω–∞ –¥–µ—Å—è—Ç–æ–º —à–∞–≥–µ –¥—Ä–æ–±–ª–µ–Ω–∏—è –∏ –ø–æ–ª—É—á–∏—Ç—å –æ—Ç–≤–µ—Ç, –ø–æ—á—Ç–∏ –Ω–µ –æ—Ç–ª–∏—á–∞—é—â–∏–π—Å—è –æ—Ç —Ç–æ—á–Ω–æ–≥–æ. –ê –ê—Ä—Ö–∏–º–µ–¥ –≤ –ø–µ—Ä–≤—É—é –æ—á–µ—Ä–µ–¥—å –±—ã–ª –ø—Ä–∞–∫—Ç–∏–∫–æ–º. –ó–∞—á–µ–º –∂–µ –æ–Ω —É–≤—ë–ª –¥—Ä–æ–±–ª–µ–Ω–∏–µ —Ñ–∏–≥—É—Ä—ã –≤ –±–µ—Å–∫–æ–Ω–µ—á–Ω–æ—Å—Ç—å?
–ê –≤–æ—Ç –∑–∞—á–µ–º. –í—ã–ø–∏—à–µ–º –∑–¥–µ—Å—å –Ω–µ—Å–∫–æ–ª—å–∫–æ –ø—Ä–æ–º–µ–∂—É—Ç–æ—á–Ω—ã—Ö –æ—Ç–≤–µ—Ç–æ–≤ –¥–ª—è –ø–ª–æ—â–∞–¥–∏ S, –∫–æ—Ç–æ—Ä—ã–µ –ø–æ–ª—É—á–∞—Ç—Å—è, –µ—Å–ª–∏ –æ—Å—Ç–∞–Ω–æ–≤–∏—Ç—å—Å—è –Ω–∞ –∫–∞–∫–æ–º-–ª–∏–±–æ —à–∞–≥–µ:
–ø–æ—Å–ª–µ 1-–≥–æ —à–∞–≥–∞ S = 1,
–ø–æ—Å–ª–µ 2-–≥–æ —à–∞–≥–∞ S = 5/4,
–ø–æ—Å–ª–µ 3-–≥–æ —à–∞–≥–∞ S = 21/16,
–ø–æ—Å–ª–µ 4-–≥–æ —à–∞–≥–∞ S = 85/54 –∏ —Ç–∞–∫ –¥–∞–ª–µ–µ.
–í–∏–¥–Ω–æ, —á—Ç–æ —Ä–µ–∑—É–ª—å—Ç–∞—Ç—ã –Ω–∞ –∫–∞–∂–¥–æ–º —à–∞–≥–µ –≤—Å—ë —É—Å–ª–æ–∂–Ω—è—é—Ç—Å—è. –ù–æ –µ—Å–ª–∏ –ø—Ä–æ–π—Ç–∏ –±–µ—Å–∫–æ–Ω–µ—á–Ω–æ–µ —á–∏—Å–ª–æ —à–∞–≥–æ–≤, —Ç–æ –æ–ø—è—Ç—å –ø–æ–ª—É—á–∏–º –ø—Ä–æ—Å—Ç–æ–π –æ—Ç–≤–µ—Ç: S = 4/3. –¢–∞–∫ —á—Ç–æ, –æ–∫–∞–∑—ã–≤–∞–µ—Ç—Å—è, –∏ —Å –ø—Ä–∞–∫—Ç–∏—á–µ—Å–∫–æ–π —Ç–æ—á–∫–∏ –∑—Ä–µ–Ω–∏—è –ª—É—á—à–µ —Å–æ–±—Ä–∞—Ç—å –≤—Å—ë –±–µ—Å–∫–æ–Ω–µ—á–Ω–æ–µ —á–∏—Å–ª–æ —Ç—Ä–µ—É–≥–æ–ª—å–Ω–∏–∫–æ–≤, —á–µ–º –æ—Å—Ç–∞–Ω–æ–≤–∏—Ç—å—Å—è –Ω–∞ –ø–æ–ª–¥–æ—Ä–æ–≥–∏.
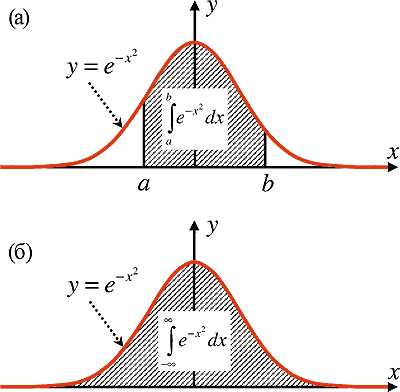
Ещё один пример. Красная линия на графике (рис. 2а), вычисляемая по формуле , — очень важная для математической статистики кривая: она выражает собой так называемое распределение Гаусса. Спрашивается, можно ли её проинтегрировать, то есть найти площадь под кривой, заключённую между числами a и b (такая площадь и называется интегралом):
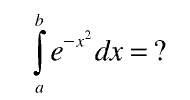
Выясняется, что нет способа точно вычислить эту площадь, как говорят, «интеграл не берётся». А если отодвинуть границы a и b в бесконечность (рис. 2б), то такой интеграл — от минус бесконечности до плюс бесконечности — вычисляется легко:
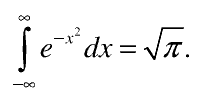
Оказывается, что это общая закономерность: если в математической или физической задаче устремить в бесконечность какую-либо величину из условий задачи, то, как правило, ответ упрощается или даже нерешаемая задача становится решаемой. Физики-теоретики особенно любят этот приём, называя его рассмотрением предельных случаев. Есть даже шутка про физика-теоретика, которого попросили рассчитать, будет ли стул стоять устойчиво. За первые пять минут он решил эту задачу для стула с одной ножкой, за следующие пять минут — для стула с бесконечным числом ножек, а потом всю оставшуюся жизнь пытался рассчитать устойчивость стула с четырьмя ножками. Примерно так и протекает жизнь теоретика.
Следующий наш пример навеян параграфом из книги «Община»: «Старые учения позитивизма заменяли достоверность очевидностью, оправдание им одно — у них не было микроскопов и телескопов, ни вниз, ни наверх. Но пытливый ум не считается с условною очевидностью, ему нужна действительность в оправе космических законов. Он понимает, что жемчуг невидим в глубине и что слои воздуха могут скрывать стаи орлов» (Община, 206).
Вот мы и попробуем взглянуть как бы в «математический телескоп» на обычную плоскость, изучаемую в школьной геометрии. Параллельные прямые, как известно, не пересекаются. Но представим себе, что где-то там, в бесконечности, они всё-таки сходятся в некоторой точке. Это легче понять, если взглянуть на эти линии как бы в перспективе. В результате получим новую геометрию, в чём-то похожую на обычную школьную геометрию Евклида, а чем-то и отличающуюся. Она называется «проективная геометрия». В ней нет расстояний, то есть нет разницы между большими и малыми отрезками. Зато к обычным прямым линиям и точкам добавлена бесконечно удалённая прямая, состоящая из бесконечно удалённых точек, причём бесконечно удалённые объекты совершенно равноправны с обычными. К сожалению, мне не удалось подобрать простого примера для иллюстрации, поэтому прошу поверить мне на слово, что проективная геометрия обладает удивительными свойствами. Можно, например, все точки заменить на прямые, а прямые — на точки, и после такой замены все теоремы останутся верными.
А теперь от взгляда в бесконечную даль перейдём к взгляду вглубь, от телескопа к микроскопу, от бесконечно большого — к бесконечно малому. Думаю, что лучшей иллюстрацией бесконечно малого будут фракталы. Что это такое? Пример «съедобного фрактала» — это некий сорт цветной капусты. Если рассмотрим его поближе, то увидим, что он состоит из «шишечек», идущих по спирали, причём каждая из них состоит из таких же маленьких «шишечек», а они, в свою очередь, — из совсем маленьких. Это свойство, когда часть подобна целому, так и называется — самоподобие. А фракталы — это самоподобные геометрические фигуры.
Но подробнее мы рассмотрим другой фрактал: знаменитое множество Мандельброта (рис. 3). Эта геометрическая фигура примечательна тем, что построена по очень простому алгоритму, который можно «зашифровать» в одной строчке (подробности см. в литературе, указанной в конце статьи):
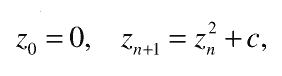
–∏ –≤ —Ç–æ –∂–µ –≤—Ä–µ–º—è –æ–Ω–∞ —Å–æ–¥–µ—Ä–∂–∏—Ç –≤ —Å–µ–±–µ –±–µ—Å–∫–æ–Ω–µ—á–Ω–æ–µ —Ä–∞–∑–Ω–æ–æ–±—Ä–∞–∑–∏–µ —Ñ–æ—Ä–º. –° –ø–æ–º–æ—â—å—é —Å–ø–µ—Ü–∏–∞–ª—å–Ω—ã—Ö –∫–æ–º–ø—å—é—Ç–µ—Ä–Ω—ã—Ö –ø—Ä–æ–≥—Ä–∞–º–º –º–æ–∂–Ω–æ —Ä–∞—Å—Å–º–∞—Ç—Ä–∏–≤–∞—Ç—å –º–Ω–æ–∂–µ—Å—Ç–≤–æ –ú–∞–Ω–¥–µ–ª—å–±—Ä–æ—Ç–∞ –≤ —Ä–∞–∑–ª–∏—á–Ω–æ–º –º–∞—Å—à—Ç–∞–±–µ, –≤ —Ç–æ–º —á–∏—Å–ª–µ –∏ –ø–æ–¥ –æ—á–µ–Ω—å –±–æ–ª—å—à–∏–º —É–≤–µ–ª–∏—á–µ–Ω–∏–µ–º. –ò –æ–∫–∞–∑—ã–≤–∞–µ—Ç—Å—è, —á—Ç–æ –ø—Ä–∏ –∫–∞–∂–¥–æ–º –ø–æ—Å–ª–µ–¥—É—é—â–µ–º —É–≤–µ–ª–∏—á–µ–Ω–∏–∏ –æ—Ç–∫—Ä—ã–≤–∞—é—Ç—Å—è –Ω–æ–≤—ã–µ –¥–µ—Ç–∞–ª–∏, –∫–æ—Ç–æ—Ä—ã–µ –±—ã–ª–∏ –ø—Ä–µ–∂–¥–µ –Ω–µ –≤–∏–¥–Ω—ã. –ù–µ—Å–∫–æ–ª—å–∫–æ —É–≤–µ–ª–∏—á–µ–Ω–Ω—ã—Ö —Ñ—Ä–∞–≥–º–µ–Ω—Ç–æ–≤ —ç—Ç–æ–π —Ñ–∏–≥—É—Ä—ã –ø–æ–∫–∞–∑–∞–Ω—ã –Ω–∞ –≤—Ä–µ–∑–∫–∞—Ö –∫ —Ä–∏—Å. 3.
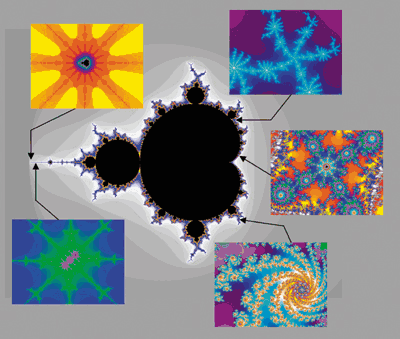
На мой взгляд, это свойство показывает, как интересно устроено пространство, в котором мы живём: в любой сколь угодно малой области пространства и даже плоскости можно обнаружить огромное разно­образие форм. В Учении есть понятие «наполненность пространства»: так, говорится, что «на самом чистом месте самый чистый снег насыщен пылью земной и космической — так наполнено пространство даже при грубом наблюдении. Добавьте множество токов и лучей, и вы получите облик действительности...» (Аум, 147). Фракталы можно рассматривать как математическую иллюстрацию наполненности пространства.
Некоторые из «пейзажей», раскрывающихся при увеличении множества Мандельброта, напоминают обитателей дна морского. Видимо, это неспроста, ведь природа построена по математическим законам. Как сказано в «Гранях Агни Йоги» (1957, 349), «мера и число есть первое основание жизни». И ещё говорится, что «каждая индивидуализированная сущность, будь то цветок, дерево, рыба, птица, животное или человек, имеет свою звуковую ноту, или вибрационный ключ, выражающийся в определённой математической формуле» (Грани Агни Йоги. VIII. 324).
Всё вышесказанное можно резюмировать так: бесконечность — очень важное и нужное понятие в математике (а следовательно, и в физике). Иногда бесконечность «спрятана» в понятиях, кажущихся с первого взгляда весьма простыми (например, в вопросе «что такое площадь фигуры?»). Часто при «устремлении в бесконечность» величин, входящих в условие задачи, её решение упрощается. Бывает, что введение бесконечных элементов в математическую теорию придаёт ей новые, весьма замечательные свойства (как, например, принцип двойственности в проективной геометрии, утверждающий «равноправие» точек и прямых). Всё это может служить поводом для размышления, проведения аналогий, попыток глубже осознать принцип Беспредельности.
–°–ø–∏—Å–æ–∫ –ª–∏—Ç–µ—Ä–∞—Ç—É—Ä—ã
–û –¥—Ä–µ–≤–Ω–µ–≥—Ä–µ—á–µ—Å–∫–æ–π –º–∞—Ç–µ–º–∞—Ç–∏–∫–µ –∏ –æ–± –ê—Ä—Ö–∏–º–µ–¥–µ:
1. –ê—Ä—Ö–∏–º–µ–¥. –°–æ—á–∏–Ω–µ–Ω–∏—è. –ú.: –§–∏–∑–º–∞—Ç–≥–∏–∑, 1962.
2. –ò—Å—Ç–æ—Ä–∏—è –º–∞—Ç–µ–º–∞—Ç–∏–∫–∏ —Å –¥—Ä–µ–≤–Ω–µ–π—à–∏—Ö –≤—Ä–µ–º—ë–Ω –¥–æ –Ω–∞—á–∞–ª–∞ XIX —Å—Ç–æ–ª–µ—Ç–∏—è / –ü–æ–¥ —Ä–µ–¥. –ê.–ü. –Æ—à–∫–µ–≤–∏—á–∞. –¢. 1. –ú.: –ù–∞—É–∫–∞, 1970.
–û –ø—Ä–æ–µ–∫—Ç–∏–≤–Ω–æ–π –≥–µ–æ–º–µ—Ç—Ä–∏–∏:
1. –ì–∏–ª—å–±–µ—Ä—Ç –î., –ö–æ–Ω-–§–æ—Å—Å–µ–Ω –°. –ù–∞–≥–ª—è–¥–Ω–∞—è –≥–µ–æ–º–µ—Ç—Ä–∏—è. –ú.: –ù–∞—É–∫–∞, 1981.
2. –•–∞—Ä—Ç—Å—Ö–æ—Ä–Ω –Ý. –û—Å–Ω–æ–≤—ã –ø—Ä–æ–µ–∫—Ç–∏–≤–Ω–æ–π –≥–µ–æ–º–µ—Ç—Ä–∏–∏. –ú.: –ú–∏—Ä, 1970.
–û —Ñ—Ä–∞–∫—Ç–∞–ª–∞—Ö:
1. –ü–∞–π—Ç–≥–µ–Ω –•.-–û., –Ý–∏—Ç—Ö–µ—Ä –ü.–•. –ö—Ä–∞—Å–æ—Ç–∞ —Ñ—Ä–∞–∫—Ç–∞–ª–æ–≤. –û–±—Ä–∞–∑—ã –∫–æ–º–ø–ª–µ–∫—Å–Ω—ã—Ö –¥–∏–Ω–∞–º–∏—á–µ—Å–∫–∏—Ö —Å–∏—Å—Ç–µ–º. –ú.: –ú–∏—Ä, 1993.
2. –®—Ä–µ–¥–µ—Ä –ú. –§—Ä–∞–∫—Ç–∞–ª—ã, —Ö–∞–æ—Å, —Å—Ç–µ–ø–µ–Ω–Ω—ã–µ –∑–∞–∫–æ–Ω—ã. –ú–∏–Ω–∏–∞—Ç—é—Ä—ã –∏–∑ –±–µ—Å–∫–æ–Ω–µ—á–Ω–æ–≥–æ —Ä–∞—è. –ò–∂–µ–≤—Å–∫, 2001.
3. Множество Мандельброта; Mandelbrot set // Онлайн-энциклопедия «Википедия» (www.wikipedia.org).
–ò—Å–ø–æ–ª—å–∑–æ–≤–∞–Ω—ã —Ç–∞–∫–∂–µ —Å–≤–µ–¥–µ–Ω–∏—è –∏–∑ —à–∫–æ–ª—å–Ω–æ–≥–æ –∏ —É–Ω–∏–≤–µ—Ä—Å–∏—Ç–µ—Ç—Å–∫–æ–≥–æ –∫—É—Ä—Å–æ–≤ –º–∞—Ç–µ–º–∞—Ç–∏–∫–∏.
Изображения фракталов построены с помощью прог­раммы ChaosPro, доступной в Интернете по адресу http://www.chaospro.de.
* –î–æ–∫–ª–∞–¥ –Ω–∞ VIII –Ý–µ—Ä–∏—Ö–æ–≤—Å–∫–∏—Ö –ß—Ç–µ–Ω–∏—è—Ö, –ù–æ–≤–æ—Å–∏–±–∏—Ä—Å–∫, 7 – 9 –Ω–æ—è–±—Ä—è 2009 –≥.
